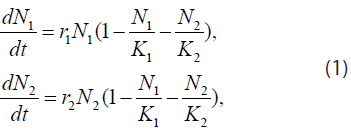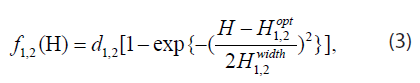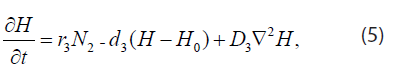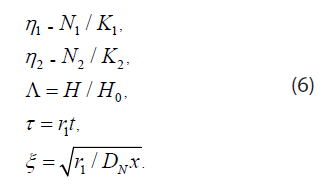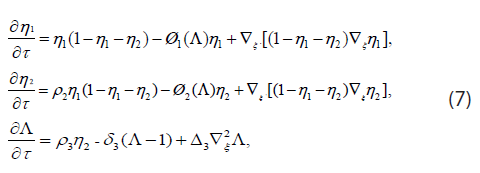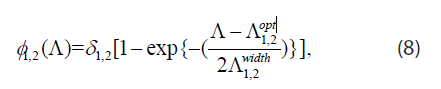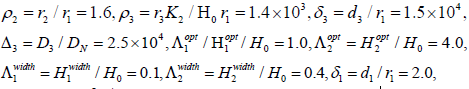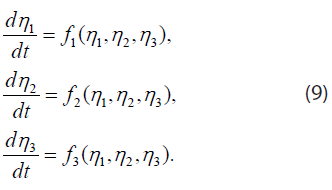Department of Physics, Temple University, Philadelphia, PA 19122, USA

*Corresponding author: Ahmed M. Fouad, Department of Physics, Temple University, Philadelphia, PA 19122, USA.

Received: June 25, 2019 Published: September 30, 2019

ABSTRACT

The acid-mediated tumor invasion hypothesis proposes that altered glucose metabolism exhibited by the vast majority of tumors leads to increased acid (H⁺ ion) production which subsequently facilitates tumor invasion [1-3]. The reaction-diffusion model [2] that captures the key elements of the hypothesis shows how the densities of normal cells, tumor cells, and excess H⁺ ions change with time due to both chemical reactions between these three populations and density-dependent diffusion by which they spread out in three-dimensional space. Moreover, it proposes that each cell has an optimal pH for survival; that is, if the local pH deviates from the optimal value in either an acidic or alkaline direction, the cells begin to die, and that the death rate saturates at some maximum value when the microenvironment is extremely acidic or alkaline. We have previously studied in detail how the death-rate functions of the normal and tumor populations depend upon the H⁺ ion density [4]. Here, we extend previous work by investigating how the equilibrium densities (at which the time rates of change of the cellular densities are equal to zero) reached by the normal and tumor populations in three-dimensional space are affected by the presence of the H⁺ ions, and we present detailed analytical and computational techniques to analyze the dynamical stability of these equilibrium densities. For a sample set of biological input parameters and within the acid-mediation hypothesis, our model predicts the transformation to a malignant behavior, as indicated by the presence of unstable sets of equilibrium densities.

KEYWORDS: Dynamical Stability Analysis; Fixed Points: Cancer Biology; Acid-Mediated Tumor invasion; Reaction-Diffusion Systems; Partial Differential Equations

INTRODUCTION

The revolutionary work of Warburg almost a century ago demonstrated that tumor cells utilize anaerobic metabolism to produce energy by converting glucose to ATP even in the presence of abundant oxygen [5]. The major disadvantage of anaerobic metabolism (when compared to the regular oxidation of glucose to CO₂ and H₂O) is the relatively low efficiency (low ATP output); however, tumor cells compensate for that by increasing the glucose flux. Moreover, FDG-PET relies basically on that glucose flux for tumor imaging purposes [6-10]. In fact, it has been well proven that the glucose consumption of tumors (primary and metastatic) is noticeably larger than normal-tissue cells [6-10]. In addition, through PET imaging, a direct relationship between tumor aggressiveness (and prognosis) and the rate of glucose uptake has been shown [6,7]. The transformation from normal to anaerobic metabolism has been directly linked to the increased acid production exhibited by tumor cells [2]. Initially, it was assumed that the lactic acid produced by anaerobic metabolism would result in an acidic intracellular pH; however, studies with NMR spectroscopy have unanimously shown that the intracellular pH of tumors is generally slightly alkaline relative to normal cells [11]. Other measurements have demonstrated that tumor cells actually excrete protons through amplification of the Na⁺/H⁺ antiporter and other membrane transporters. As a result, it is now clear that the extracellular pH of tumors is substantially lower (usually by about 0.5 pH unit) than normal [12-15]. Generally, a persistent pH below about 7.1 results in death of normal cells due to a p53-dependent apoptosis pathway triggered by increased caspase activity [16,17]. However, tumor cells are much more tolerant to acidic pH, presumably due to mutations in p53 or other components of the apoptotic pathway. In fact, tumor cells typically exhibit a maximum proliferation rate in relatively acidic mediums (i.e. pH 6.8) [18-20]. As a consequence, it has been concluded that the invasiveness of tumors are directly attributed to the acidification of their microenvironments, which, in turn, makes it ideal for tumor cells to proliferate and, moreover, corroborates the death of normal cells that compete against tumor cells for glucose and substrate; because of their relatively high intolerance of these acidic microenvironments.

An acid-mediated tumor invasion hypothesis (AMTIH) has been developed [1-3], wherein microenvironmental changes at the tumor-host interface caused by altered metabolism in transformed cells (accelerated uptake of glucose due to increased reliance on glycolysis) lead to an excess acid production, thus facilitating tumor invasion. Concurrent with this increase inglucose consumption is the up-regulation of the Na⁺/H⁺ antiport system [21,22]. The resulting net increase in tumor intracellular pH leads to normalization, and therefore to a decrease in extracellular pH by about 0.5 pH unit compared to normal tissue [11-13,15,20]. While some investigators have attributed this increased reliance on glycolysis to the existence of a compromised tumor blood supply leading to poor O₂ perfusion of tumor tissue [23], others have found evidence that it is a phenotypical consequence of transformation [24]. 

The reaction-diffusion model of the AMTIH [2] predicts the degree to which excess hydrogen ions in the tumor interstitium diffuse into the surrounding tissue. It also predicts the extent of the zone of altered interstitial pH found at the tumor-host interface. This microenvironment is harmful to normal tissue because of three reasons. First, normal cell viability declines sharply below extracellular pH of 7.1 [11-13,15,20]. Second, an acidic microenvironment stimulates production of enzymes which degrade the extracellular matrix [25,26]. Third, diminished pH results in loss of intercellular gap junctions reducing the cohesion, collaboration, and communication among normal cells at the tumor edge [27]. This altered microenvironment leads to a progressive loss of normal cells and degradation of extracellular matrix. This subsequently allows tumor cells (which are much more resistant to acidic extracellular pH) to invade the host tissue. Eventually, the acid-mediation hypothesis of tumor invasion is supported by recent reports that high lactate levels are directly correlated with the likelihood of metastases, tumor recurrence, and restricted patient survival [28].

The main research focus in this paper is to investigate how the equilibrium densities reached by the normal and tumor populations are affected by the existence of the H⁺ ions. To achieve that, given some sample values of biological input parameters (which are patient-specific), we present a detailed approach (that utilizes both analytical and computational techniques) to solving numerically for the equilibrium points (fixed points) that represent the equilibrium densities at which the normal, tumor, and acid populations could coexist in three-dimensional space. Moreover, through solving numerically for the eigenvalues of the Jacobian matrix of the partial differential equations that represent how the three populations evolve with time, we determine the dynamical stability of these fixed points. 

This article is outlined as follows. In Sec. 2 we review the previous work on modeling tumor growth and invasion. The canonical Gatenby-Gawlinski reaction-diffusion model that captures the key components of the AMTIH is presented in Sec. 3. In Sec. 4 we present our analytical and computational results on the dynamical stability analysis of the reaction-diffusion model. The conclusions and outlook are presented in Sec. 5.

PREVIOUS WORK

Tumor growth and other biological systems are particularly amenable to modeling with cellular automata. This approach has been used increasingly since Wolfram (1986) demonstrated that every automaton with local interactions belongs to one of a small number of universality classes [29]. Some of the earliest work in tumor modeling with cellular automata was carried out by Düchting and Vogelsaenger to investigate the effects of different radio-therapeutic strategies on tumor growth [30,31].

More recently, Qi et al. [32] developed a cellular automaton model of tumor growth which includes immune system surveillance and accounts for mechanical pressure from within the tumor. This model is of interest because it reproduces the Gompertz growth law. The cellular automaton approach was also employed by Smolle and Stettner [33], and by Smolle [34,35] in an attempt to infer relationships between tumor morphology and basic biological features; such as cell cohesion, motility, and autocrine and paracrine growth factors. Kansal et al. [36,37] have made use of the Voronoi tessellation of space in a cellular automaton model of brain tumor growth dynamics. This elegant approach allows for the preservation of the discrete nature of cells (or groups of cells); but removes the anisotropy of a regular lattice.

Cellular automata have also been used to model neoangiogenesis, which is another crucial aspect of cancer biology. Chaplain and Anderson [38,39] have used cellular automata to solve the discrete version of a system of non-linear partial differential equations which describe the response in space and time of endothelial cells to tumor angiogenesis factor and fibronectin, including migration, proliferation, anastomosis, and branching. Cellular automata have also been used to model the development of leaf veins, insect trachea, and tumor neovascularization [40].

Some models that use systems of partial differential equations have been developed to simulate tumor growth and invasion; such as tumor angiogenesis [38,39,42,46], post-surgical response to tumor removal [41], avascular tumor growth [43,44], tumor cell motility during invasion [45], and drug resistance and vascular structure in chemotherapy [47]. All these models (either automaton-based or continuum, stochastic or deterministic) simulate one or more aspects of cancer biology. Other models, including chemotherapeutic agent transfer [47] and diffusive vasculature for nutrient transfer [48], do so with a spatially-uniform term accounting for delivery or removal, not by including individual vessels distributed throughout space.

Reaction-diffusion model of tumor invasion

Gatenby and Gawlinski propose that the alteration of microenvironmental pH induced by the tumor’s anaerobic metabolism may provide a simple, yet complete mechanism for cancer invasion. In this section, we extend a reaction-diffusion model they developed, which describes the spatial distribution and temporal development of tumor tissue, normal tissue, and excess H⁺ ion density [2]. A pH gradient across the tumor-host interface is proposed by the model, which is verified by experimental data. A transition from benign to malignant growth, analogous to the adenoma-carcinoma sequence, is predicted by the model through investigating the dynamics of the tumor-host interactions. This transition is controlled through the effects of many biological parameters. Moreover, it is crucial to pinpoint that the applicability of their model is limited to the vicinity of the tumor-host interface. 

All realistic models should include as fundamental factors properties common to almost all tumors, regardless of their originating genetic instability and heterogeneity. One fundamental cellular dynamic is that tumor cells evolve away from the original differentiated state toward one that is more primitive (less ordered). Metabolic changes adapt to this evolution by increasing reliance on glycolytic metabolism (even in the presence of abundant oxygen) despite the 19-fold reduction in energy production that comes as a consequence [2]. The Gatenby-Gawlinski model proposes that it is specifically this energy-production inefficiency associated with that altered metabolism that corroborates successful tumor invasion, particularly the transformation-induced reversion of neoplastic tissue to primitive glycolytic metabolic pathways with a consequent increased acid production and the diffusion of the resulting acidic protons into neighboring normal tissue. That very acidic microenvironment is what eventually corroborates tumor invasion which is relatively more tolerant to it than normal cells. The following temporal sequence can be concluded after all. Initially, high H⁺ ion concentrations in tumors diffuse into neighboring normal tissue, exposing these normal cells to tumor-like interstitial pH. Next, normal cells immediately adjacent to the tumor edge are incapable of surviving in this chronically acidic environment. Eventually, the progressive loss of layers of normal tissue at the tumor-host interface facilitates tumor invasion.

From the temporal sequence mentioned above, we can conclude that the invasion mechanism capitalizes primarily on the low interstitial pH of tumors (resulting from the anaerobic metabolism) and the subsequent, relatively low viability of normal tissue in an acidic environment favorable to tumor tissue. The Gatenby-Gawlinski model mathematically frames the acid-mediation hypothesis as a system of reaction-diffusion equations whose solutions could precisely predict the structure and dynamics of the tumor-host interactions.

The acid-mediated tumor invasion hypothesis described above can be represented by the following system of reaction-diffusion equations. Let N₁ and N₂ denote the cell densities in cell/cm³ of the normal and tumor populations, respectively. Assuming these populations only compete for available space, their temporal evolution is governed by the equations

where r_1,2 and K_1,2 are the growth rates in s^-1 ( s denotes second) and spatial carrying capacities in cell/cm3 of the respective populations. Moreover, if we propose a diffusion model similar to the Fickian one, where the diffusion parameters are themselves density-dependent [maximum value in vacant space and zero in high concentrations (close-packed cells)], then Eq. (1) becomes 

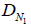
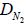
where  and in cm²/s are the empty-space diffusion constants of the normal and tumor cells, respectively. For simplicity we assume that these are approximately equal: 

The Lotka-Volterra terms ensure that the density-dependent diffusion parameters are always positive-definite  [49].

Next, the model assumes that each cell has an optimal pH for survival, and that if the local pH deviates from the optimal value (either in the acidic or alkaline direction), the cells start to die. In addition, it proposes that the death rate saturates at some maximum value when the environment is extremely acidic or alkaline. A simple ad-hoc functional form meeting these criteria is the “inverted Gaussian”

where H is the local concentration of H+ ions in mol/L, d_1,2 are the saturated death rates in s^-1, H opt are the local H⁺ ion concentrations in mol/L, corresponding to the optimal pH’s, and H width are the half-widths of the “inverted Gaussian” in mol/L. Substituting the death rates (3) into (2) we obtain

The H⁺ ions are produced at a rate proportional to the local concentration of tumor andremoved by the combined effects of buffering and vascular evacuation, both of which are proportional to micro-vessel areal density. Thus

where H is the H⁺ ion concentration in mol/cm³, r₃ is the H⁺ ion production rate in mol/(cell *s), d₃ is the H⁺ ion uptake rate in ^s-1, H₀ is the H⁺ ion concentration in serum, and D³ is the H⁺ ion diffusion constant in cm²/s. 

Eq. (4) and (5) can be rewritten in terms of the variables

In dimensionless form Eq. (4) and (5) become

where ρ₂ = r₂ / r₁, ρ₃ = r₃ K / (H₀ r₁),δ₃ = d₃ / r₃ , ∆₃=D₃ / D_N. The death-rate functions are dimensionless and have the form

where 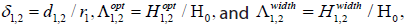 are all dimensionless as well.

For in vitro spheroids, doubling times are between 1 and 4 days. Therefore, this yields r₂ = ln 2/2.5 days ≈ 2.0 x 10^-6/s. For normal tissue wound healing, 4 days seem reasonable for the doubling time; thus, r₁ = ln 2/4.0 days ≈ 2.0 × 10⁶/s . The volume-limited carrying capacities of tumor and normal tissues are assumed to be the same and given by K₁ = K ≈ 5 × 10⁸ cells/cm³. For vascular evacuation without buffering d₃ = αp, where α ≈ 200/cm is the vessel areal density and p ≈ 1.2 × 10⁴ cm/s is the vessel permeability for lactate, resulting in a removal rate of 2.4 ×10^-2/s . Local buffering might increase this by 25%. Thus, the final estimate for this rate is d₃ ≈ 3.0 ×10^-2/s. If the serum pH₀ = 7.4 is also the optimal pH for normal tissue growth, then H1opt = H0 3.98 × 10^-11 mol/cm³. An optimal pH of 6.8 for tumor growth gives H2opt=1.58 × 10^-10 mol/cm³. 

As for acid production rate, if a tumor is sufficiently large, then the temporal and spatial derivatives at its core are small. From Equation (5) we see that r₃ ≈ d₃ (H_core− H₀)/ K2. Assuming a core pH of 6.4, this yields r ≈ 2.2 × 10^-20 mol/(cell*s). This last value is remarkably consistent with the curve fit results of the Martin-Jain data to the old model [50]. The lactic acid and cellular diffusion constants are D₃ ≈ 5 × 10^-6 cm²/s and D_N ≈ 2 × 10^-10 cm²/s, respectively. 

Using the values above, the numerical estimates of the dimensionless parameters in Eq. (7) and (8) are as follows: 

and δ₂ = d₂ / r₁ = 2.0. The last four values are admittedly guesswork; but it is reasonable to choose the saturated death rates greater than the growth rates and the width of the optimal pH region for tumor cells greater than that for normal cells.

Equilibrium densities and dynamical stability analysis

Here, we present a detailed technique we developed to solve for the fixed points of the reaction-diffusion system defined in Eq. (7), with the sample numerical values of the biological input parameters given in Sec. 3, and determine their dynamical stability. The significance of the fixed points is that they determine equilibrium densities of the normal, tumor, and acid populations at which they could coexist in three-dimensional space (if no malignant behavior is already in progress). The dynamical stability of the fixed points can be determined by solving numerically for the eigenvalues of the Jacobian matrix. If all eigenvalues are negative, the fixed point is considered to be stable; however, if one or more of the eigenvalues is (are) positive, the fixed point is considered to be unstable. A stable fixed point represents an intermediate balance between the normal, tumor, and acid populations where none of them is likely to undergo any noticeable growth into the other two; however, an unstable fixed point where tumor cells are very likely to invade normal tissue upon any slight perturbations of the cellular densities could potentially develop into a malignancy. Note that in Equation (7), we present multiple reaction and diffusion factors that could contribute to a change in the cellular densities of the three populations. By mathematical definition, if the fixed point is stable, after slight changes in the equilibrium cellular densities (due to e.g. cellular diffusion) have taken place, the cellular densities tend to converge infinitesimally back to their initial equilibrium values (so the time rates of change of the cellular densities remain at zero after all); however, on the other hand, in an unstable fixed point, after the occurrence of slight perturbations in the equilibrium cellular densities, significant divergences off the equilibrium values are very likely to take place (that is, the cellular populations are not necessarily expected to converge back to their initial values), where malignancies are very likely to develop upon any small perturbations of unstable fixed points; because the presence of the acid specifically would always significantly catalyze the process in the direction where tumor invasion into normal tissue takes place (not vice versa).

Note that, when the microenvironment is extremely acidic, the death rate of tumor cells saturates at a value considerably lower than its counterpart for normal cells, and this is interpreted as tumor cells being more capable of surviving in an extremely acidic microenvironment [2,4].

We find the fixed points and analyze their dynamical stability as follows. If we restrict our attention to solutions η₁, η₂, and η₃ ≡ Λ, which depend on time but are independent of the spatial coordinate ξ, Eq. (7) reduce to three coupled ordinary differential equations

The fixed points or points of equilibrium are points (η₁^*, η₂^*, η₃^*) where the right sides of Equation (9) vanish. Near a fixed point, the differential equations may be linearized in the form 

Substituting η_j −η_j^* = a_j e^λt, one finds n exponential solutions, with λ and a_j given by the eigenvalues and eigenvectors of the matrix 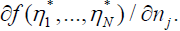 If all n of the eigenvalues λ are negative, η −η^* decays exponentially with time, and the fixed point is “stable”. If one or more of the λ values is (are) positive on the other hand, the fixed point is unstable. Note that variables η₁ (t), η₂ (t), and Λ(t) depend on t but not on the coordinate ξ. 

Next, we solve numerically for the fixed points. To find the fixed points, we set the derivatives in the cellular equations [the first and second of Eq. (7)] equal to zero after eliminating Λ using the acid equation [the third in Eq. (7)]. This yields two non-linear equations in two unknowns, namely η₁ and η₂, which are physically contained within the interval [0,1]. Therefore, we partition the domain 0 ≤ η₁≤ 1 ⊗ 0 ≤ η₂ ≤ 1 into a rectangular grid with ∆η = ∆η = 0.01 (10000-points grid), and use these 10000 points as numerical inputs for a multi-dimensional Newton’s algorithm. For a specific Newton’s solution for η₁ and η₂, η₃ is found using the third equation in (7). We determine the stability of the resulting solutions by numerically computing the eigenvalues of the Jacobian matrix (we have published the software package we used to perform the dynamical stability analysis presented here [4]). The fixed- points analysis for the parameters given in the previous section is shown below [4,51] in Table 1. Fixed point 3 is stable (all eigenvalues are negative). Fixed point 4 is unstable (some eigenvalues are positive) and is very likely to develop into a malignancy upon any slight perturbations of the equilibrium cellular densities [note that when η₁ is zero, this means that all the normal population has died at the interface (microenvironment) joining the three populations]. Fixed points 1, 2, and 5 are all unstable and unphysical (negative density values). Note that the existence of two different physical solutions (either stable or unstable) means that for the biological input parameters given in Sec. 3, wherever the normal, tumor, and acid populations are found in a dynamical equilibrium in three-dimensional space, it must be in one of these two solutions [note that we are not reporting here trivial fixed points such as (0,0,1) and (1,0,1)].

Fixed Point	Eigenvalues	Stable/Unstable
(− 0.26500634, 0.01500634, 1.14005922)	(− 1.500000e+04, 1.205189e−01, 1.205189e−01)	Unstable (unphysical)
(− 0.23499366, − 0.01500634, 0.85994078)	(− 1.500000e+04, 1.295203e−01, 1.295203e−01)	Unstable (unphysical)
(0.00000000, 0.37206032, 4.47256298)	(− 1.498978e+04, − 1.081070e+01, −1.372060e+00)	Stable

The canonical Gatenby-Gawlinski model of the acid-mediated tumor invasion hypothesis presented in Sec. 3 shows how the densities of normal cells, tumor cells, and excess H⁺ ions change due to two factors: first, local chemical reactions between the three populations and, second, density-dependent diffusion by which these populations spread out in space. According to the hypothesis, the dominant mechanism for cancer invasion is the tumor-induced alteration of microenvironmental pH. Moreover, the hypothesis predicts an acidic pH gradient extending into the peritumoral normal tissue, where the normal mammalian cells (but not tumor cells) are intolerant of acidic interstitial pH in the range typically found within this gradient. 

DISSCUSSION, CONCLUSIONS, AND FUTURE WORK

In Sec. 4 we have developed detailed analytical and computational techniques to analyze the dynamical stability of the Gatenby-Gawlinski reaction-diffusion system by solving for the fixed points of the differential equations [see Eq.  (7)] that represent how the normal, tumor, and acid populations evolve with time, then determining the stability of these fixed points by solving for the eigenvalues of the Jacobian matrix. The significance of the fixed points is that they determine possible densities at which the normal, tumor, and acid populations could coexist in dynamical equilibrium in three-dimensional space (if no malignant behavior is already in progress; that is, the time rates of change of the densities of the three populations are equal to zero). As for the dynamical stability of the fixed points, if all eigenvalues are negative, the fixed point is stable; however, if one or more of the eigenvalues is (are) positive, the fixed point is unstable. In a stable fixed point, after slight changes in the equilibrium cellular densities have taken place (due to e.g. cellular diffusion), the cellular densities tend to converge infinitesimally back to their initial equilibrium values (so the time rates of change of the cellular densities remain at zero after all); however, on the other hand, in an unstable fixed point, after the occurrence of slight changes in the equilibrium densities, significant divergences off the initial equilibrium values are likely to take place, where malignancies are likely to emerge; because, on balance, the presence of the acid specifically would always significantly corroborate the process into only one direction; that is, tumor invasion into normal tissue (not vice versa). Whenever a malignant behavior is already in progress, this implies that the time rate of change of the density of tumor cells is positive. A fixed point (either stable or unstable) physically represents an intermediate balance between the three populations where none of them is undergoing any noticeable growth into the other two. If the fixed point is stable, a malignant behavior is unlikely to emerge, even after the occurrence of slight perturbations of the equilibrium cellular densities at the interface (microenvironment) joining the three populations. On the other hand, an unstable fixed point where tumor cells are very likely to invade normal tissue upon any slight perturbations of the equilibrium cellular densities could potentially develop into a malignancy. Note that, in the reaction-diffusion model we present here, from a mathematical standpoint and within the acid-mediation hypothesis, only the dynamical stability of the equilibrium points (not the initial equilibrium density values) controls whether a prospective malignant behavior is likely; because the dynamical stability by itself controls what happens after any slight perturbations of the initial equilibrium density values have taken place. We have solved numerically for the fixed points (and their dynamical stability) of the reaction-diffusion system presented in Eq. (7) with the sample numerical values of the biological input parameters provided in Sec. 3. As demonstrated in Table 1, for physical fixed points (all density values are positive), our numerical results show that both stable (fixed point 3) and unstable (fixed point 4) configurations are possible. For the particular set of the biological input parameters we have operated on in Sec. 3, the existence of two different physical solutions means that wherever the three populations are found in a dynamical equilibrium in three-dimensional space, it must be in one of these two solutions.

As for future work, it would be interesting to study systematically how the fixed-point behavior depends on the biological input parameters. In simple systems this can be done analytically; but in systems as complex as the one introduced in Eq. (7), numerical methods are needed. Possibly, one can use numerical algorithms [52], designed to compute branches of stable and unstable solutions, and compute the Floquet multipliers that determine stability along these branches. The initial starting points for the computation of periodic orbits are generated automatically at the Hopf bifurcation points. Such techniques can also locate folds, branch points, period-doubling bifurcations, and bifurcations to tori. Along branches of periodic solutions, branch switching is possible at branch points and at period-doubling bifurcations.

Once the bifurcation diagrams in parameter space are understood in this way, dynamical simulations can be performed to determine tumor growth or regression rates.

Acknowledgment

I am grateful to Dr. Edward Gawlinski and Dr. Theodore Burkhardt for very thoughtful comments and discussions. 

REFERENCES

1. Gatenby RA. (1991). Population ecology issues in tumor growth. Cancer Res. 51(10):2542-2547.
2. Gatenby RA, Gawlinski ET. (1996). A reaction-diffusion model of cancer invasion. Cancer Res. 56(24):5745-5753.
3. Patel AA, Gawlinski ET, Lemieux SK, Gatenby RA. (2001). A cellular automaton model of early tumor growth and invasion: the effects of native tissue vascularity and increased anaerobic tumor metabolism. J Theor Biol. 213(3):315-331.
4. Fouad  A. (2015). Density-dependent diffusion models with biological applications: Numerical modeling and analytic analysis. Doctoral dissertation, Temple University.
5. Warburg O, Wind  F, Negelein E. (1927). The metabolism of tumors in the body. J Gen Physiol. 8(6):519-530.
6. Di Chiro G, Hatazawa J, Katz DA, Rizzoli HV, De Michele DJ. (1987). Glucose utilization by intracranial meningiomas s an index of tumor aggressivity and probability of recurrence: a PET study. Radiology. 164(2):521-526.
7. Haberkorn U, Strauss LG, Reisser CH, Haag D, Dimitrakopoulou A, Ziegler S, et al. (1991). Glucose uptake, perfusion, and cell proliferation in head and neck tumors: relation of positron emission tomography to flow cytometry. J Nucl Med. 32(8):1548-1555.
8. Hawkins RA, Hoh C, Glaspy J, Choi Y, Dahlbom M, Rege S, et al. (1992). The role of positron emission tomography in oncology and other whole-body applications. Semin Nucl  Med. 22(4):268-284.
9. Patz Jr EF, Lowe VJ, Hoffman JM, Paine SS, Harris LK, Goodman PC. (1994). Persistent or recurrent bronchogenic carcinoma: detection with PET and 2-[F-18]-2-deoxy-D-glucose. Radiology. 191(2):379-382.
10. Yonekura Y, Benua RS, Brill AB, Som P, Yeh SD, Kemeny NE, et al. (1982). Increased accumulation of 2-deoxy-2-[18F]fluoro-D-glucose in liver metastasis from colon cancer. J  Nucl Med. 23(12):1133-1137.
11. Griffiths JR. (1991). Are cancer cells acidic? British journal of cancer. 64(3):425-427.
12. Gillies RJ, Liu Z, Bhujwalla Z. (1994). 31P-MRS measurements of extracellular pH of tumors using 3-aminopropylphosphonate. Am J Physiolo. 267(1 pt 1):C195-C203.
13. Martin GR, Jain RK. (1994). Noninvasive measurement of interstitial pH profiles in normal and neoplastic tissue using fluorescence ratio imaging microscopy. Cancer Res. 54(21):5670-5674.
14. Martin GR. Thesis; Pittsburgh, PA: Carnegie Mellon University, Pittsburgh, 1995.
15. Stubbs  M, Rodrigues L, Howe FA, Wang J, Jeong KS, Veech RL, et al. (1994). Metabolic consequences of a reversed pH gradient in rat tumors. Cancer Res. 54(15):4011-4016.
16. Park HJ, Lyons JC, Ohtsubo T, Song CW. (1999). Acidic environment causes apoptosis by increasing caspase activity. Br J Cancer. 80(12):1892-1897.
17. Williams AC, Collard TJ, Paraskeva C. (1999). An acidic environment leads to p53 dependent induction of apoptosis in human adenoma and carinoma cell lines: Implications for clonal selection during colorectal carcinogenesis. Oncogene. 18(21):3199-3204.
18. Rubin H. (1971). pH and population density in the regulation of animal cell multiplication. The Journal of cell biology. 51(3):686-702.
19. Dairkee SH, Deng G, Stampfer MR, Waldman FM, Smith HS. (1995). Selective cell culture of primary breast carcinoma. Cancer Res. 55(12):2516-2519.
20. Casciari JJ, Sotirchos SV, Sutherland RM. (1992). Variations in tumor cell growth rates and metabolism with oxygen concentration, glucose concentration, and extracellular pH. J Cell Physiol. 151(2):386-394.
21. Bierman AJ, Tertoolen LG, De Laat SW, Moolenaar WH. (1987). The Na+/H+ exchanger is constitutively activated in P19 embryonal carcinoma cells, but not in a differentiated derivative. Responsiveness to growth factors and other stimuli. Journal Biol Chem. 262(20):9621-9628.
22. Kaplan DL, Boron WF. (1994). Long-term expression of cH-ras stimulates Na-H and Na (+)-dependent Cl-HCO3 exchange in NIH-3T3 fibroblasts. Journal Biol Chem. 269(6):4116-4124.
23. Vaupel P, Kallinowski F, Okunieff P. (1989). Blood flow, oxygen and nutrient supply, and metabolic microenvironment of human tumors: a review. Cancer Res. 49(23):6449-6465.
24. Smith TAD. (2000). Mammalian hexokinases and their abnormal expression in cancer. Br J Biomed Sci. 57(2):170-178.
25. Kato Y, Nakayama Y, Umeda M, Miyazaki K. (1992). Induction of 103-kDa gelatinase/type IV collagenase by acidic culture conditions in mouse metastatic melanoma cell lines. J Biol Chem. 267(16):11424-11430.
26. Rozhin J, Sameni M, Ziegler G, Sloane BF. (1994). Pericellular pH affects distribution and secretion of cathepsin B in malignant cells. Cancer Res. 54(24):6517-6525.
27. Yamasaki H. (1991). Aberrant expression and function of gap junctions during carcinogenesis. Environ Health perspect. 93:191-197.
28. Walenta S, Wetterling M, Lehrke M, Schwickert G, Sundfor K, Rofstad EK. (2000). High lactate levels predict likelihood of metastases, tumor recurrence, and restricted patient survival in human cervical cancers. Cancer Res. 60(4):916-921.
29. Wolfram S. (1986). Theory and applications of cellular automata. World scientific. 1:560.
30. Düchting W, Vogelsaenger T. (1984). Analysis, forecasting, and control of three-dimensional tumor growth and treatment. J M Syst. 8(5):461-475.
31. Düchting W, Vogelsaenger T. (1985). Recent progress in modelling and simulation of three-dimensional tumor growth and treatment. Biosystems. 18(1):79-91.
32. Qi AS, Zheng X, Du CY, An BS. (1993). A cellular automaton model of cancerous growth. J Theor Biol. 161(1):1-12.
33. Smolle J, Stettner H. (1993). Computer simulation of tumour cell invasion by a stochastic growth model. J Theor Biol. 160(1):63-72.
34. Smolle J. (1998). Fractal tumor stromal border in a nonequilibrium growth model. Anal Quant Cytol Histol. 20(1):7-13.
35. Smolle J. (1998). Cellular automaton simulation of tumour growth–equivocal relationships between simulation parameters and morphologic pattern features. Anal Cell Pathol. 17(2):71-82.
36. Kansal AR, Torquato S, Harsh GR, Chiocca EA,  Deisboeck TS. (2000). Simulated brain tumor growth dynamics using a three-dimensional cellular automaton. J Theor Biol. 203(4):367-382.
37. Kansal AR, Torquato S, Harsh GR, Chiocca EA, Deisboeck TS. (2000). Simulated brain tumor growth dynamics using a three-dimensional cellular automaton. J Theor Biol 203(4):367-382.
38. Chaplain MA,  Anderson AR. (1995). Mathematical modelling, simulation and prediction of tumour-induced angiogenesis. Invasion  metastasis. 16(4-5):222-234.
39. Anderson AR, Chaplain MA. (1998). Continuous and discrete mathematical models of tumor-induced angiogenesis. Bull Math Biol. 60(5):857-899.
40. Markus M, Böhm D, Schmick M. (1999). Simulation of vessel morphogenesis using cellular automata. Math Bio Sci. 156(1-2):191-206.
41. Adam JA. (1997). General aspects of modeling tumor growth and immune response. A survey of models for tumor-immune system dynamics. 15-87.
42. Olsen L, Sherratt JA, Maini PK, Arnold F. (1997). A mathematical model for the capillary endothelial cell-extracellular matrix interactions in wound-healing angiogenesis. IMA J Math, Appl Med Biol. 14(4):261-281.
43. Ward JP, King JR. (1997). Mathematical modelling of avascular-tumour growth. IMA J Math,Appl Med Biol. 14(1):39-69.
44. Ward JP, King JR. (1999). Mathematical modelling of avascular-tumour growth II: modelling growth saturation. IMJ J Math Appl Med Biol. 16(2):171-211.
45. Perumpanani AJ, Norbury J. (1999). Numerical interactions of random and directed motility during cancer invasion. Mathematical and computer modelling. 30(7-8):123-133.
46. Sleeman BD, Anderson ARA, Chaplain MAJ. (1999). A mathematical analysis of a model for capillary network formation in the absence of endothelial cell proliferation. Applied mathematics letters. 12(8):121-127.
47. Jackson TL, Byrne HM. (2000). A mathematical model to study the effects of drug resistance and vasculature on the response of solid tumors to chemotherapy. Math Biosci. 164(1):17-38.
48. Byrne HM, Chaplain  MA. (1995). Growth of nonnecrotic tumors in the presence and absence of inhibitors. Math Biosci. 130(2):151-181.
49. Pao CV. (2014). A Lotka-Volterra cooperating reaction-diffusion system with degenerate density-dependent diffusion. Nonlinear Analysis: Theory, Methods & Applications. 95:460-467.
50. Martin GR, Jain RK. (1994). Noninvasive measurement of interstitial pH profiles in normal and neoplastic tissue using fluorescence ratio imaging microscopy. Cancer Res. 54(21):5670-5674.
51. Fouad AM. (2018). A kinetic view of acid-mediated tumor invasion. Eur  Biophys J. 47(2):185-189.
52. Doedel EJ, Paffenroth RC, Champneys AR, Fairgrieve TF, Kuznetsov YA, Oldeman BE, et al. (2002). AUTO 2000: CONTINUATION AND BIFURCATION SOFTWARE.

Copyright: Fouad AM. ©2019. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Citation: Fouad AM (2019). Dynamical Stability Analysis of Tumor Growth and Invasion: A Reaction- Diffusion Model. Oncogen 2(4): 20.